第 7 章原则

“情况的确如此，我在这方面有直觉。偶尔也会出现一些较复杂的案子，那我就得忙碌一阵子，亲自去查访一番。要知道，我有许多特殊知识，可以用来解开这些谜团，而且能轻易地解决问题。那篇文章中讨论的推理的原则，让你很鄙视，但对我的实际工作却是无价之宝。敏锐的观察力是我的第二天性。我们俩第一次见面时；我说起你是从阿富汗来的，你那时似乎很惊讶哩。”

— 柯南·道尔《血字的研究》

从技术角度来说，作图是一件很容易的事情，但作一幅好的统计图形则并非易事，它需要一些指导原则。那么图形优劣的评判标准是什么？最直接的标准就是，读者能否通过图形清楚地了解数据中的信息。这涉及到对读者群体的心理学研究和对数据的反复思考，比如，饼图和条形图分别用角度和长度来表达数值大小，那么人眼对角度和长度的感知精度是一样的吗？心理学调查结果显示并非如此：人眼对角度的感知较差。迄今为止，专门做过统计图形方面的心理学研究的统计学家寥寥无几，其中成果最显著的当属 Cleveland (1985) ，本章也主要基于他的一些观点进行总结与展开。

7.1 数据至上

数据是宝贵的，它们也许来自艰辛的问卷调查，或是繁琐的实验测量，因此我们应该尽量珍惜，但现实状况是我们经常有意或无意糟蹋数据，这样的情形包括：表达数据的元素被次要图形元素遮挡，数据的特征无法在图中凸显，或者数据经过了不恰当的人工处理等。

7.1.1 分清主次

对于一幅图形而言，显然并非所有的图形元素都同等重要。例如，散点图中的点应该是最重要的元素，等高线图中的线更重要，等等。因此，我们不能让次要的图形元素干涉数据的表达，要让图形显得干净、清晰。主要元素的外观要仔细选择，使数据在图中占有最重要的视觉地位，而不会被标签等元素遮挡或干涉。用 Cleveland 的话说，就是要让数据突出来（stand out）。

R 基础图形系统中默认的点的样式是空心点，在很多情况下这并不是一个好的选择，因为空心点在图中看起来太不起眼，尤其是数据点较少的时候。我们延续 6.2.5 小节中的美剧演员收入数据，在这里讨论如何突出主要元素。图 7.1 是演员收入与电视剧评分的散点图，左图使用了默认的空心点，右图使用了实心点。这批数据的样本量只有 72，左图中的点所用的墨水可能和坐标轴等次要元素差不多，所以数据在图中也显得不够突出，而实心点则很明显占据了一幅图的视觉重心。

par(mfrow = c(1, 2))
data("tvearn", package = "MSG")
plot(pay/10^4 ~ rating, data = tvearn, ylab = "pay (10^4)") # 默认为空心点
plot(pay/10^4 ~ rating, data = tvearn, pch = 19, ylab = "pay (10^4)") # 改为实心点

图 7.1: 演员收入与电视剧评分的空心和实心散点图：右图的视觉冲击力更强。

这两幅图实际上有个共同的问题，就是图中空白区域太大，这是由最高收入的那位演员引起的。这种情况也从一定程度上降低了图形元素的表达效率，因为我们放眼望去，一幅图的一半区域都是空白，绝大部分点都集中在图的下半部分。当然，在这个问题上我们也不能绝对化，因为有时候这种大片空白能反衬处离群点 — 取决于我们要显示的重点是什么。当图中存在离群点时，解决办法之一就是取对数，这种办法能减轻数量级的影响，数据越大，则被拉向原点的幅度越大。我们都知道，取对数的前提条件是数字全都大于零，正好本例中的收入数据满足这个条件。对收入取过对数之后的散点图如图 7.2 上图，由于此时纵坐标的刻度意义变了，我们在读图的时候需要了解数字 n 实际上代表的是 $10^{n}$，例如 6 与 5 的差距并非 1，而是 10 倍，即 $10^{6-5}$。

如果我们关心的对象是收入和评分的关系，那么一幅散点图就足够了；如果我们还想进一步从图中了解每个点代表的演员是谁，那么我们就需要往图中加文本标签。标签是有很强显示力的工具，它能直截了当告诉我们信息，然而由于它的体积相对较大，若处理不当，反而会让图中充满文本信息，从而失去了数据本身的意义。在本例中添加姓名标签不容易做到自动化，即自动安排标签的位置让它们不要重叠，因为本身这幅图中的点就已经有重叠，不过 maptools 包中的 pointLabel() 函数提供了基于模拟退火算法和遗传算法的添加标签方案，它能尽量做到不让标签重叠。事实上即使用这些算法来添加标签，也仍然会出现大量的遮挡现象，如图 7.2 下图，这也是受本书版面大小所限，读者可以运行代码在更大的图形窗口中查看结果，重叠程度应该会轻一些。

par(mfrow = c(1, 2), mar = c(3.2, 3.6, .05, .05))
plot(log10(pay) ~ rating, data = tvearn, pch = 19)
plot(log10(pay) ~ rating, data = tvearn, pch = 20, ylab = "", col = "red")
library(maptools)

## Loading required package: sp

## Checking rgeos availability: TRUE

with(tvearn, pointLabel(rating, log10(pay), labels = actor, 
                        cex = .6, col = "#00000099", xpd = TRUE))

图 7.2: 取对数的收入与评分散点图以及演员名称：纵轴的收入数据经过了以 10 为底的对数处理；下图中加上了演员的名称。

顺便提一下，关于文本标签的使用，多维标度分析（Multidimensional Scaling，MDS）是一个非常适合以标签展示为主的统计学方法。简言之，MDS 的思想是将高维空间中个体之间的距离在低维空间中尽量准确地表达出来，这里的低维空间通常是二维平面。因为我们关心的重点是个体与个体之间的距离，那么最好将个体的某种特征画在图中，最直接的想法当然就是个体的名称，此时图的重点就是这些名称标签，所以尽管标签的背后对应着坐标点，我们也不必把点画出来，甚至坐标轴都可以完全去掉。图 7.3 是 6.2.3 小节提到过的音乐数据的 MDS 平面图，这幅图没有坐标轴，也没有点，只有曲目名称，这就足够了，因为这些名称之间的距离就是它们在标准化之后的原始数据上的距离（注意原始数据有 10 个变量，这里降维为 2），从图中我们可以很快看出曲目之间的相似性。

data("music", package = "MSG")
par(mar = c(0, 2, 0, 0))
# 标准化所有频率变量到 0-1 之间并计算曲目之间欧式距离
st.music <- apply(music[, -(1:2)], 2, function(x) {
  (x - min(x)) / (max(x) - min(x))
})
fit <- cmdscale(dist(st.music))
plot(fit, type = "n", ann = FALSE, axes = FALSE)
text(fit[, 1], fit[, 2], rownames(music), cex = .7, xpd = TRUE)

图 7.3: 音乐数据的多维标度分析平面图：Eels 的 Saturday Morning 离所有曲目最远，维瓦尔第的 V8 也比较独特。

关于图形元素主次关系，还牵涉到一些细节设置问题，这也是我们在附录 B 介绍那么多图形细节的原因之一。例如，坐标轴的刻度短线的方向默认朝外（tcl 参数），这是合理的设置，如果刻度线朝内伸去的话，就可能会干涉到作图区域的元素；又如 xaxs 和 yaxs 参数，它们默认会先让作图区域的范围向外扩展 4%，这样坐标轴和作图数据的边界之间就留出了一片小空间，数据中的最小值和最大值都不会紧贴坐标轴，也能让主要图形元素充分显示出来，不受坐标轴线的干扰。

7.1.2 符号明确可分

我们经常遇到需要在图中表达分组信息的情况，如图 3.4，此时我们应该选择差异最大的外观，以免各组数据无法区分开来。例如空心圆圈和空心方框的区别就不够显著，但空心圆圈和实心圆圈就有很明显的区别。为了检验两种符号是否有足够的区分度，我们可以用 MSG 包中的 char_gen() 函数生成一个字符方阵，看我们是否能从中快速找出不同的字符，例如 O 和 Q 很相似，所以从一群 Q 的方阵中找一个 O 可能就很困难，但从一群 Q 中找星号*则要容易得多：

char_gen(c("O", "Q"), n = 320, nrow = 8) # 从 Q 中找 O

## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQOQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ

char_gen(c("*", "Q"), n = 320, nrow = 8) # 从 Q 中找 *

## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ*
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ

关于符号使用的问题，Robinson (2003) 是一篇很好的参考短文，这里我们不再深入介绍，但是要提醒注意的是，尽管我们可以小心挑选外形差别大的符号，当数据分组数目特别大的时候这种努力往往过犹不及，因为人眼的识别能力毕竟有限，太多太杂的符号混在同一幅图中很可能无法清楚表达任何信息，仅仅是制造图形垃圾而已。

7.1.3 谨慎处理数据

通常数据只有经过处理才能揭示我们想要知道的信息，例如给我们全国所有人的身高数据只会让我们被淹没在数字中，但一个均值或者中位数就能告诉我们身高的平均水平。人们可能因为这个原因形成了处理数据的习惯，但这对于统计图形来说往往是灾难，宝贵的原始信息被毁灭于人为处理。在图形中，我们提倡尽量表达原始数据，而不要人为处理数据，包括不要省略数据，以及不要离散化数据。

Cleveland (1985) 中给了一个省略数据的例子，可以看作是 1986 年美国挑战者号航天飞机失事的原因之一，大意是航天局的工程师们在发射之前研究了 O 型环的故障与温度的关系，他们看的是一幅散点图，横轴为温度，纵轴为 O 型环发生故障的数量，从散点图中来看，温度与这个零件的故障数量并没有什么联系，然而最终挑战者号还是因为温度原因发射失败并解体爆炸。那么这幅散点图有什么问题呢？首先，它只画出了零件失效的情况，而省略了零件未失效的那些观测数据，退一步讲，他们的散点图中即使没有观察到零件失效与温度的关系，也不能代表温度与零件不失效没有关系，而事实是如果把零件未失效的数量和相应的温度加上去的话，我们就能观察到低温情况下 O 型环容易发生故障；其次，这幅散点图中的温度范围不够大，而发射当前的气温是 31 华氏度（零下 1 摄氏度），属于超低温，这样的情况也没有在以往数据中观察到，因此这个发射行动是非常鲁莽的。

图形相比起表格的优势之一就是它能以较小的空间展示很多信息，10 行数据和 1000 行数据占用的空间可能没有区别，而表格则不然，数据越多就需要更大的空间展示。我们几乎没有必要刻意删减原始数据再画图，即使需要删减，通常也应该在看完全局数据之后再决定看局部数据。

离散化数据是人们更常用的数据处理手段，并且这种手段的缺点更不容易被发觉。所有离散化，就是将原本连续的数据人为分组，例如，将年龄分为 0-5 岁、5-10 岁、……。作者猜想这种处理方式一方面是陈旧的计算手段留下来的糟粕，因为分组统计更容易计算，另一方面也是受一些基于分类数据统计方法的引诱，例如列联表的各种“精美”分析，换句话说，我们在拿方法硬套数据。为什么我们不推荐将连续数据离散化？原因非常简单：连续数据包含的信息比离散数据多，离散化处理会损失信息。或者通俗解释：你问一个人的年龄，若得到的回答是“20 岁到 50 岁之间”，你必然觉得不够满意。

图形中的离散化现象很普遍，如 4.39 小节的风向图就是一个例子，当然风向图中的离散化也许有一定道理。更多情况下是不必要的离散化，如根据不同年龄组计算身高的均值，这种情况下我们完全可以画身高和年龄（连续变量）的散点图，此时身高和年龄的关系一目了然，而不需要从一组组均值中去看它们的关系。更严重的问题是，离散化的分组往往带有任意性，我们可以按 5 岁一个区间分组，也可以按 10 岁一个区间，这种任意性的存在可能会导致结果的截然不同，甚至让我们得出相反的结论。

set.seed(319)
x <- rnorm(100)
y <- rnorm(100)
par(mfrow = c(1, 2)) # 以下 cut_plot() 函数来自 MSG 包
cut_plot(x, y, c(-2.02, -0.9, -0.3, 1, 2, 2.5), col = "gray")
cut_plot(x, y, c(-2.02, 0, 0.25, 0.5, 2.8, 3), col = "gray")

图 7.4: 任意离散化连续数据得到的不同结果：左右散点图中数据完全相同，只是离散化分组区间不同，导致趋势截然不同。

图 7.4 展示了离散化数据的一种弊病：左右两幅图中的数据完全相同，只是两幅图中我们用了不同的分组区间去将变量 x 离散化为 5 组，竖着的虚线表示分组的端点，在每一组内我们计算 y 的均值并连线，左图中我们看到数据有下降趋势，右图则显示为上升趋势，而事实是 x 和 y 是独立的，毫无关系。这就像盲人摸象的故事 — 有人摸到了耳朵说它像扇子，有人摸到了尾巴说像绳子。

同样我们也不能将“不处理数据”这条原则绝对化，有一种情况下处理数据会让图形表达更清楚，那就是从原始数据中不易直接观察的数据，例如两条折线的差异，或两组数据均值的差异，或观察增长率。谢益辉 (2010) 分别使用等方差和异方差假设对同一批数据作了 t 检验并得到 P 值，为了比较这两组 P 值的差异，作者将它们作差再画图，原因是绝大多数 P 值都非常接近，若直接画两组 P 值的散点图，那么得到的几乎是一条直线，看不出差异，而作差之后，差异就变得很明显了。这样的数据处理并没有改变原始数据的性质，只是将同样的数据换一种形式表达，没有损失任何信息。读者可以再回顾第 1 章中的图 1.1，这幅图可以换个角度来表达，即画出出口减去进口的值，这样只需要和 0 对比就知道顺差逆差的情况了。

还有一种可能需要略微处理数据的情况，就是当数据中重叠的点很多时，我们要想办法让读者能够读出这些重叠的信息，随机略微打乱数据点的位置是一种处理办法（参见图 6.1），尽管它看起来修改了原始数据，但只要经过充分的解释说明，读者应该不会被误导；如果我们不处理数据，当然也有办法表达这些重叠信息，如 4.5 小节。

实际应用中我们常常还会遇到一种“无意识的处理数据”，即原始数据并没有经过任何中间处理，但最终画到图中的时候被无意识地改变了意义。这一点我们在 6.2.3 小节中曾经提到过，即“事后诸葛亮”的做法。当我们已知图中元素分类信息的时候，我们可以用一些特殊标记（如颜色）来表达这个信息，当分类信息未知时，我们就需要慎重了，典型的应用如聚类分析，有时候聚类结果可能比较牵强，但经过给数据标记颜色的处理，读者会被刻意引导到特定结论上。后面 7.5 小节我们再看例子。

7.2 节约墨水

谈到墨水问题，我们不得不提及可视化大师级人物 Edward Tufte，他发明了一个有趣的词，叫图形垃圾（chartjunk），所谓的图形垃圾就是一幅图形中的多余元素，它们对表达数据毫无帮助，甚至掩盖或歪曲数据中的信息。我们身边的图形垃圾实在数不胜数，例如毫无意义的渐变色背景（有人可能会争论这是为了美观考虑），或者用复杂的图形表达简单的数据。

Cleveland 也有类似的观点，提倡用尽量简单的图形元素表达尽量多的数据信息；用更量化的指标来说，就是“数据/墨水比”要尽量高，意思是用少的墨水打印出多的数据。Cleveland 提出他的点图（4.11 小节）也有此考虑，因为点图中的图形元素占用的空间小，但和条形图一样能表达出数字的大小。

Tufte (2001) 中提到一个浪费墨水的极端例子，他本人的评论为“它可能是史上出版物中最糟糕的图形”（This may well be the worst graphic ever to find its way into print），这幅图由《美国教育》杂志发表，如图 7.5 所示。这幅看起来很炫目的图到底画了什么？其实只是 5 个数字，记录了 1972 到 1976 年中，25 岁及以上的美国大学生录取比例；该图的标题为“大学新生年龄结构”，而这个所谓的“结构”分两类，一类是 25 岁及以上的新生，另一类是 25 岁以下的，这两个比例相加为 100%，图下半边代表了 25 岁及以上的学生，这 5 个比例分别为 28.0%、29.2%、32.8%、33.6% 和 33.0%，这便是这幅三维立体图形要表达的全部，图的上半边是下半边的“倒影”。Michael Friendly 在他的数据可视化网站（http://www.datavis.ca/）中也给出了评价：

一幅图形可以用三种手段之一来装潢，一是让人眼花缭乱的颜色，二是 3D 效果，三是伪装得就像有丰富的内容一样，而这幅图动用了全部三种手段。

通过这一则例子，相信读者可以深刻体会到什么是图形垃圾。

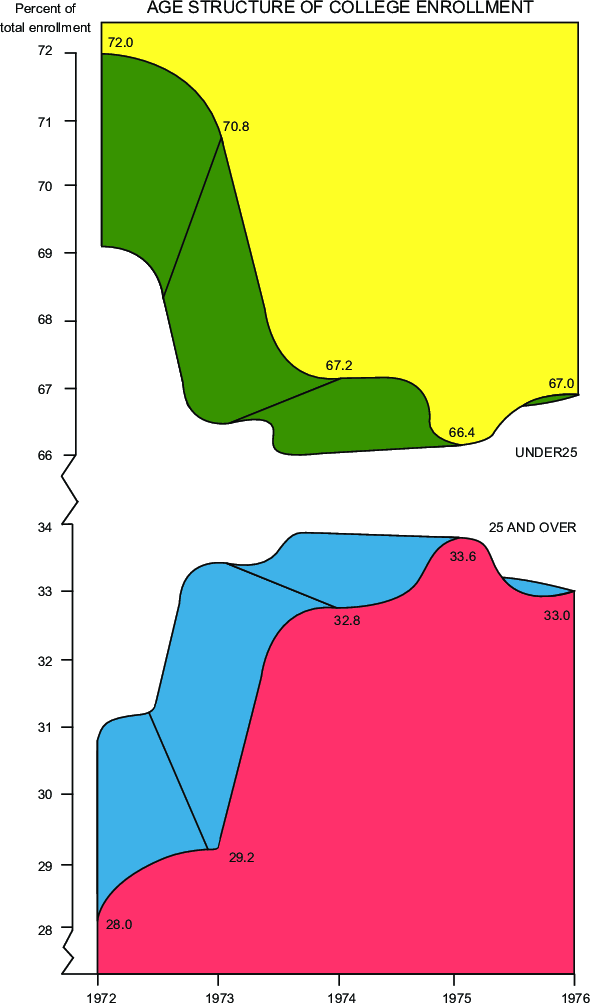
图 7.5: 史上最糟糕的图形垃圾：一幅超级复杂的图形，一共表达了 5 个数字，即 1972 年到 1976 年中，25 岁及以上的美国大学新生比例。

7.3 设计布局

这里说的布局主要指 B.2 小节提到的纵横比，它是一个对图形解释非常重要的概念，尤其是折线图。简单来说，纵横比影响的是图形元素宽高的比率。“瘦高”的图中，折线的斜率大，给人的感觉是升降趋势非常剧烈，而“矮胖”的图中，趋势变化则看起来平缓一些。

layout(matrix(1:2, 2), heights = c(2, 1))
par(mar = c(4, 4, 0.1, 0.1))
plot(sunspots)
plot(sunspots, asp = .1)

图 7.6: 不同纵横比设置下的太阳黑子时序图：上图没有特别的纵横比设置，下图的 asp 参数为 0.1，从下图可以看出太阳黑子数量随着时间上升比下降速度更快。

R 基础图形系统中通常用 asp 参数设置纵横比，下面我们给一个经典例子来说明它的作用。图 7.6 是 1749 到 1984 年太阳黑子数量的时间序列图，数据为月度数据。我们都知道太阳黑子的数量有周期性，其周期大约为 11 年，这一点在图中可以很容易看出来（折线有规律地起伏）。图 7.6 上图使用的是默认纵横比设置，即纵横比随着图形大小自动调整，而下图中固定为 0.1，初看起来这两幅图没有什么不同，但下图揭示了一个重要的发现：太阳黑子数量上升时的速度比下降的速度更快，注意观察图中上升的折线比下降的折线更陡峭，而上图中则很难看出这个现象，因为折线斜率太大。关于图 7.6 我们要补充说明的是，下图并不是简单地把高度压缩了一下而已，即使图形的高度更高，图中的折线形状也不会变化，关于这一点读者可以自行验证。

Cleveland 对这个问题的建议是调整纵横比让所有的折线的倾斜角度平均值接近 $45\,^{\circ}$（banking to $45\,^{\circ}$），因为人眼对 $45\,^{\circ}$ 附近的角度感知最精确，而对太大或者太小的角度感知都很差，例如图 7.6 中为什么我们更难看出上图中的折线角度差异？

纵横比是一个很有用的调整图形感观的工具，换句话说，用它来撒谎也是很容易的，不过如今的读者应该都能识破这种小伎俩了。

7.4 附带解释

尽管我们说“一图胜千言”，但图形本身对于不同读者来说可能会有不同的解读，甚至有些读者未必能理解一幅图的真正意思，这时候就很有必要提供附带文字解释。附带解释有两种方式，一种是向图中加上文本标注，这种方式有很大的局限性，因为图的空间毕竟有限，而且过多的文本标注可能会使图形本身失去重心（7.1.1 小节）；另外一种方式就是图的标题，据作者的观察，这一点在英语文献中似乎做得相对好一些，图形通常有明确的标题，而且标题就像一段完整的话，但大多数中文文献中的图都惜字如金，图的标题只有一句话，关于图的解释通常放在正文中，这种做法可能会让读者无法专注于图形的阅读，因为需要不断回到正文结合相应的解释文字来理解图形。

理想情况下，一幅图配上相应的标题文字解释，应该能够形成一个相对独立而完整的故事。但话说回来，如果一幅图需要太多的文字解释，那么这幅图本身的设计质量也值得怀疑，作者可能需要考虑简化图形。本书中大部分图形都遵循了添加详细标题文字解释的原则。从技术上而言，这只是 LaTeX 中 figure 环境的 \caption{} 而已。

7.5 考虑心理

图形中有许多的心理因素需要考虑，相信读者应该看过一些关于视觉欺骗的图片，图 7.7 就是一个经典示例，其实红线和黑线一样长，但由于箭头方向内外朝向的问题，使得红线看起来更长。类似的心理因素还包括：

set.seed(320)
par(mar = c(1, 0, 1, 0), xpd = TRUE)
plot.new()
h <- runif(4)
v <- runif(4, 0, .4)
arrows(v[1:2], h[1:2], v[1:2] + .6, h[1:2], angle = 45, code = 3)
arrows(v[3:4], h[3:4], v[3:4] + .6, h[3:4], angle = 135, code = 3, col = 2)

图 7.7: 一个经典的视觉欺骗示例：红线和黑线谁更长？

红色为夸张色，所以红色区域可能看起来比实际大小更大
大区域中的填充颜色看起来比小区域更深一些
同一个角度在不同方向上放置可能会导致它看起来不一样，例如从水平线出发的角度和从 $45\,^{\circ}$ 角出发的同一个角看起来大小不同，这会影响饼图的解读

Cleveland (1985) 在一些心理学实验基础上将一系列视觉判断任务按照人眼感知精度从高到低排了以下顺序：

位置
长度
斜率和角度
面积
体积
颜色（顺序：色调、饱和度和亮度）

根据这个顺序，散点图和 Cleveland 点图表达的信息最精确，因为我们看的是点的位置，而气泡图表达信息则不太精确，因为我们要看气泡的面积。

以上的研究结论当然很重要，但这里我们还要指出另一种影响心理的做法。7.1.3 小节提到了对数据附加标记的做法，这在聚类分析中尤其常见，并且它也对人的心理有很大的影响。例如，从原散点图中我们根本看不出聚类现象，但经过颜色或其它方式标注，我们被无意识引导到了聚类现象上。图 7.8 就是这样的例子：数据完全是没有规律的随机数，如果我们对它做 K-Means 聚类，结果如左图；如果做 $\alpha$ 凸包计算，结果如右图。表面上看来，这些随机数中似乎有规律，但实际上我们看到的都是假象。左图用不同样式的点作了标记，所以看起来上下分别有聚类；右图因为有连线的存在，诱使我们认为图中有个“空心”。$\alpha$ 凸包由 alphahull 包 (Pateiro-Lopez, Rodriguez-Casal, and. 2019) 生成，详细原理我们就不在这里介绍了，大意是从散点图中根据一个参数 $\alpha$ 的取值找出所有的凸包（convex hull，用一个圈包住一些点），$\alpha$ 越小则找到的凸包越多，反之越少。

set.seed(320)
par(mfrow = c(1, 2))
x <- matrix(rnorm(200), ncol = 2)
plot(x,
  pch = c(4, 19)[kmeans(x, centers = 2)$cluster],
  xlab = expression(x[1]), ylab = expression(x[2])
)
library(alphahull)
plot(ahull(x, alpha = 0.4), xlab = expression(x[1]), ylab = expression(x[2]))

$不存在聚类的 K-Means 聚类散点图（左）和 $\alpha$ 凸包（右）$

图 7.8: 不存在聚类的 K-Means 聚类散点图（左）和 $\alpha$ 凸包（右）

7.6 统计原则

对统计图形来说，自然也应该有统计学上的考虑，这些考虑说到底仍然是以“尊重数据”为核心。本节用两个例子来说明统计图形中应该考虑的一些统计原则，一是直方图，二是误差线图。

直方图实际上也是对数据离散化分组，所以它不可避免有一定的随意性，只是这里的分组有一定的理论背景，并非像 7.1.3 小节中提到的例子那样没有章法、毁灭信息。无论如何，它还是隐藏了原始数据，因此我们认为在画直方图（包括移动平均直方图）时，若有可能，则尽量加上密度曲线，或者坐标轴须（4.20 小节），因为密度曲线不受分组区间的影响，坐标轴须能反映原始数据的位置。试想，若有一大批数据集中正好在某个分组边界上，那么这个边界点归于左边组或右边组会在很大程度上影响直方图的形状，而在密度曲线上则会显示出这里有较高的密度值。

误差线图似乎是统计学工作者极为常用的一种图形，本书没有介绍它，因为这种图形对数据的毁灭程度往往更高。误差线图通常是一个连续变量对一个分类变量画的图，基于分类变量的每个类别，分别计算连续变量的均值 $\bar{X}$ 及标准差 $s$，然后用短横线标记出 $\bar{X}\pm m\cdot s/\sqrt{n}$ 的位置，其中 $n$ 是组内样本量，$m$ 是一个倍数，可以是 1 或 2 或其它数字，这样做的原因是短横线的标记表达了均值的置信区间（置信度取决于 $m$，例如 $m=2$ 时大约是 95% 置信区间）。当然，这种做法理论上没有什么不对，但问题就在于原本我们有所有的连续变量数据，而误差线图把这些数据压缩为了均值和标准差，严重损失了数据信息；如果我们更挑剔一点，$\bar{X}\pm m\cdot s/\sqrt{n}$ 作为置信区间是需要假设条件的（如正态分布等），为什么我们一定要用这个需要假设前提的对称的区间呢？

Koyama (2010) 给出了一个很好的例子来说明误差线图的弊端，这里我们也可以模拟类似的数据。图 7.9 展示了一幅误差线图（左）和它背后的真实数据（右）。如果只看误差线图，那么我们的印象可能是 A 组和 B 组的分布一样，因为它们的均值相同（条形图的高度代表均值），均值的标准误也相同（误差线的高度代表 2 倍的标准误），C 组和 D 组也一样。真实情况是 A、B、C、D 组背后的数据分布大不相同：A 组为均匀分布，样本量 20，B 组只有 2 个点，C 组由 1 个离群点和剩下聚成一团的 9 个点构成，D 组由两类点构成。对数据的压缩掩盖了这些完全不同的分布情况。

尽管直方图和误差线图都很流行，但读者也需要慎重考虑其使用。借用统计学家 Frank Harrell Jr 的话，“就像人有人权一样，数据也有数据权，请尊重数据权。”

set.seed(321)
par(mfrow = c(1, 2), mar = c(4, 4, .5, .1))
y <- c(runif(20), c(.43, .54), c(.6, runif(9, .3, .4)), 
       c(runif(6, .5, .6) - .12, runif(4, .15, .22) + .12)) - .2
x <- factor(rep(LETTERS[1:4], c(20, 2, 10, 10)))
mid <- barplot(m <- tapply(y, x, mean), col = 1:4, ylim = c(0, .4))[, 1]
s <- 2 * tapply(y, x, sd) / sqrt(table(x))
arrows(mid, m - s, mid, m + s, code = 2, col = 1:4, angle = 90, length = .15)
stripchart(y ~ x, vertical = TRUE, method = "jitter", pch = 20)

图 7.9: 误差线图的弊端：左图为常见的误差线图，右图是误差线图背后的完整数据。

7.7 思考与练习

我们可以把 7.1.2 小节中的找 O 和找 * 的任务当作一个游戏请你的朋友来玩，若有可能，请记录下他 / 她完成这两个任务分别使用的时间以及相关背景信息（在不侵犯隐私的情况下）并发给作者；或者用 MSG 包中的 char_gen() 函数生成更多任务去玩。
Cleveland 提出了 4.11 小节介绍的 Cleveland 点图，它的优势之一是数据 / 墨水比相对较高，因为一个点占用的面积比一个矩形条要小得多，看起来这些点也表达了和条形图等量的信息。仔细观察 Cleveland 点图，你认为它是否“让数据突出出来”了？或者你认为点图读起来方便吗？
Lane and Sándor (2009) 是一篇相对较新的关于作图原则的论文，它总结了不少有用的原则，请阅读这篇论文并考虑其中的原则是否都有足够的说服力。例如作者建议通常情况下不要用背景颜色，而我们知道 ggplot2 系统的图形通常都带有灰色背景，它们是否有冲突？
Michael Friendly 的数据可视化网站是一个具有丰富图形资源的网站，尤其值得称道的是他对统计图形历史的资料总结，同时他也给了很多劣质图形的例子，比如某杂志封面上关于康奈尔大学的学费和排名折线图（http://www.datavis.ca/gallery/context.php），可以说是极具误导性，请仔细阅读这些案例，并寻找我们身边的杂志和媒体中有哪些糟糕的统计图形。
压缩数据导致损失信息并不是统计图形特有的现象，我们身边经常能看到这种例子。比如我们看到一些重要的统计数据只公布均值的时候，甚至觉得不平，感觉就像“被（均值）代表”了一样。我们应该采取怎样的行动让人们拥有足够的保护原始数据的意识？

参考文献

———. 1985. The Elements of Graphing Data. Monterey, CA: Wadsworth.

Koyama, Tatsuki. 2010. Beware OF Dynamite. http://biostat.mc.vanderbilt.edu/twiki/pub/Main/TatsukiRcode/Poster3.pdf.

Lane, D. M., and A. Sándor. 2009. “Designing Better Graphs by Including Distributional Information and Integrating Words, Numbers, and Images.” Psychological Methods 14 (3): 239–57. https://doi.org/10.1037/a0016620.

Pateiro-Lopez, Beatriz, Alberto Rodriguez-Casal, and. 2019. Alphahull: Generalization of the Convex Hull of a Sample of Points in the Plane. https://CRAN.R-project.org/package=alphahull.

Robinson, Heman. 2003. “Usability of Scatter Plot Symbols.” Statistical Computing and Graphics Newsletter 14 (1). http://stat-computing.org/newsletter/issues/scgn-14-1.pdf.

———. 2001. The Visual Display of Quantitative Information. 2nd ed. Cheshire, CT, USA: Graphics Press.

———. 2010. “统计图形和模拟视角下的模型理论解析.” Master’s thesis, 中国人民大学. http://1t.click/ajnW.

第 7 章 原则